快速排序 - QuickSort

Published: August 26, 2017

• Categories:
• 算法 2

• Tags:
• Algorithms 2
• Java 9

快速排序可能是应用最广的排序算法了，这里来简单分析一下这个算法。

设计思路

快速排序算法的设计思路是基于分治的：

1. 选取一个元素作为切分元素 pivot，然后基于 pivot 把数组切分成三部分：左子数组（元素小于等于 pivot ），pivot，右子数组（元素大于等于 pivot ）。
2. 递归地对左右两个子数组进行快速排序，只要保证左右两个子数组分别有序了，整个数组也就有序了。

维基百科上面的一个动画，比较形象地解释了这个过程：

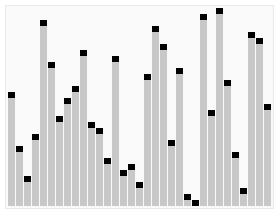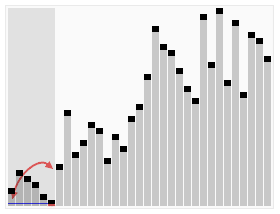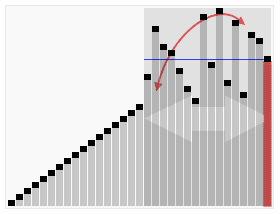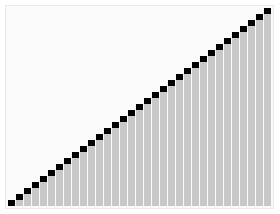
实现

如下是快排的一个 Java 实现：

public class QuickSort {
    public static void sort(Comparable[] a) {
        StdRandom.shuffle(a);
        sort(a, 0, a.length - 1);
    }

    private static void sort(Comparable[] a, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        int j = partition(a, lo, hi);
        sort(a, lo, j - 1);
        sort(a, j + 1, hi);
    }
}

主要的排序逻辑就是一个简单的递归，所以算法的核心在切分算法 partition 上。

一种切分的思路是这样的：

1. 选取 a[lo] 作为切分元素 pivot，用一个指针 i从 lo+1 开始向右遍历数组，遇到一个大于等于 pivot 的元素就停下，再用一个指针 j 从 hi 向左遍历，遇到一个小于等于 pivot 的元素就停下。
2. 这时候 i 和 j 位置的元素显然是错位的，交换之，这样就保证了 i 左侧的元素都是小于 p 的，j 右侧的元素都是大于 p 的。
3. 重复步骤 1 和 2 ，直到 i 和 j 相遇（或者某一个指针遍历了全部元素），就表示数组已经切分完毕，此时只需要把 p 和左侧元素的最大值，也即是 a[j] 交换位置即可。

如下是 partition 方法的实现：

private static int partition(Comparable[] a, int lo, int hi) {
    Comparable pivot = a[lo];
    int i = lo, j = hi + 1; 
    while (true) {
        while (++i < hi && a[i].compareTo(pivot) < 0); 
        while (--j > lo && a[j].compareTo(pivot) > 0); 
        if (i >= j) {
            SortUtil.exchange(a, lo, j); 
            return j;
        }
        SortUtil.exchange(a, i, j);
    }
}

几个问题

代码看起来没什么问题，但是细节是魔鬼，有几个有意思的问题：

++i还是i++？

这么写有没有问题？

int i = lo + 1, j = hi; 
    while (true) {
        while (i++ < hi && a[i].compareTo(pivot) < 0); 
        while (j-- > lo && a[j].compareTo(pivot) > 0); 

其实是没问题的，但是这么写的话， i 和j在遍历过程中停在的位置其实是 “下一个要检查的元素” ，对应的交换代码就得这么写：

if (i >= j) {
    SortUtil.exchange(a, lo, j + 1);
    return j;
}
SortUtil.exchange(a, i - 1, j + 1);

这会平白多出了几个 +1 和 -1，略微降低了些可读性，所以最好还是使用 ++i/--j 的方式。

< 还是 <= ?

目前的 i, j 遍历规则是：在不越界的情况下，是只要当前元素 < pivot，i就会递增；同样的，只要当前元素 > pivot，j 就会递减。

如果分别改为 <= 和 >= 呢？

这不会导致排序错误，但是按照书上的说法，这种方式会在处理只有少数几种取值数据时的性能会比较差，可以通过数学证明此时的算法时间复杂度是平方级别（然而我不会。。）。

小心边界

很容易犯得一个错误是忽略了边界情况，比如 a[lo] 是数组最大的元素时，i就会一路向右根本停不下来，直到 ArrayIndexOutOfBoundsException，所以需要划定边界 i 不能超过 hi。 要注意，如果 i 是因为到达 hi 而终止了遍历，那么对于 i 这次遍历，a[hi] 这个元素实际上是没有被检查过的，大于、小于还是等于 pivot 都是未知的，但是好在 j 第一个要检查的元素就是 a[hi]，所以还能可以保证 a[hi] 被检查到的。

给j划定边界是冗余的，因为当 j 到了 lo 位置时，一定有 a[j].compareTo(pivot) == 0，循环就会终止。

循环终止条件

当i和j完成对整个数组的扫描时，切分完成，此时我们需要跳出循环，我们的算法实现里是判断当 i >= j 时即终止，为什么呢？

仔细研读一下除了终止条件以外的代码：

    while (true) {
        while (++i < hi && a[i].compareTo(pivot) < 0); 
        while (--j > lo && a[j].compareTo(pivot) > 0); 
        if (...) {
            // 遍历完成准备跳出循环
            ...
        }
        SortUtil.exchange(a, i, j);
    }

上述代码里其实隐含了这么一个不变式： i 和 j 遍历完成准备跳出循环时，i左侧的元素都是 < pivot 的，j 右侧的元素都是 > pivot 的。

因此当 i 和 j 相交时，就完成了对整个数据就完成了扫描，需要终止循环，分两种情况分析：

1. 如果 i > j ：此时一定是 i = j + 1，这是因为 i 左侧的元素都是 < pivot 的，j 右侧的元素都是 > pivot，不可能一个元素夹在 i 和 j 之间，既 > pivot 又 < pivot。同样，由于 i 位于 j 的右侧，所以有 a[i] > pivot，由于 j 位于 i 的左侧，所以有 a[j] < pivot，所以此时交换 lo 和 j 位置是合理的。
2. 如果 i = j ：这种情况有两种可能性：
   1) i 由于到达边界 hi 而停下，j 由于判断 a[j] <= pivot 而停在了 hi 位置。所以有 a[j] = a[hi] <= pivot，交换 lo 和 j 位置是合理的。
   2) i 由于判断 a[i] >= pivot 而停下，同时 j 由于判断 a[j] <= pivot 而停下，此时有 a[i] = a[j] = pivot，交换 lo 和 i/j 都是合理的。

综上，可以把终止条件写成：

        if (i >= j) {
            SortUtil.exchange(a, lo, j); 
            return j;
        }

小心死循环

因为个人对于 ++i/i++ 这种技巧不太喜欢，我最开始写的 partition 代码是这样子的：

private static int partition(Comparable[] a, int lo, int hi) {
    Comparable pivot = a[lo];
    int i = lo + 1, j = hi; 
    while (true) {
        while (i < hi && a[i].compareTo(pivot) < 0) {
            i++;
        }
        while (j > lo && a[j].compareTo(pivot) > 0) {
            j--;
        }
        if (i >= j) {
            SortUtil.exchange(a, lo, j);
            return j;
        }
        SortUtil.exchange(a, i, j);
    }
}

这样写其实有一个很严重的 bug，那就是在 i 和 j 同时遇到和 pivot 相同的元素时会造成死循环，考虑这种情况，需要 partition 的数组是：[1 5 1 3 1 2] ，pivot = 1, lo = 0, hi = 5。

i 在遍历到 lo+2 时发现 a[lo + 2] >= pivot，就会停下来，同理 j 会停在 hi - 1 上，然后 i 和 j 位置上的元素互换，也就是两个 1 互换，没有任何实际效果，然后 i 和 j 依然停在原位置，继续互换……这样就进入了死循环。

所以为了避免这种情况，关键就在于互换相同元素之后，要保证 i 和 j 能够继续遍历而不是停在当前位置上，最后一行做出如下修改即可：

private static int partition(Comparable[] a, int lo, int hi) {
    Comparable pivot = a[lo];
    int i = lo + 1, j = hi; 
    while (true) {
        ...
        SortUtil.exchange(a, i++, j--);
    }
}

特性分析

快速排序的性能取决于切分的效率。如果每次正好从中间切分，可以通过数学证明时间复杂度是 O(NlgN)，但是实际中的数据未必如此完美，根据概率统计的运行时间一般在 1.39NlgN 左右。

但是如果最初的数组已经有序，这是最坏的情况，此时算法实际上就约等于选择排序了，时间复杂度变为 O(N^2)，所以排序开始会先随机打乱数组以尽量避免最坏情况。

快速排序是不稳定的，稍微思考一下代码实现就可以想清楚这一点。在Java语言中，Arrays.sort() 方法对于基本类型的排序使用的就是改造版的快速排序，但是 Object 类型的排序往往要求稳定性，所以用的是归并排序。

改进

1. 递归方法执行到到数组长度比较小时（5~15之间），切换到插入排序，因为此时插入排序效率更高。
2. 不再使用 a[lo] 作为切分元素，二是从数组中取3个数，用它们中间的那个作为切分元素。
3. 三向切分：把数组切分为三部分，分别对应小于，等于，大于。这又是一个很有意思的算法，这里贴出代码，就不再仔细解释了：

   public class ThreeWayQuickSort {
   
    public static void sort(Comparable[] a) {
        StdRandom.shuffle(a);
        sort(a, 0, a.length - 1);
    }
   
    private static void sort(Comparable[] a, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        Comparable v = a[lo];
        int lt = lo, gt = hi, i = lo + 1;
        while(i <= gt) {
            int cmp = a[i].compareTo(v);
            if (cmp < 0) {
                SortUtil.exchange(a, lt++, i++);
            } else if (cmp > 0) {
                SortUtil.exchange(a, i, gt--);
            } else {
                i++;
            }
        }
        sort(a, lo, lt - 1);
        sort(a, gt + 1, hi);
    }
   }
   

参考

• 《算法》（第四版）2.3 快速排序
• 维基百科 - 快速排序